Gerak lurus berubah beraturan atau GLBB adalah gerak lurus yang kecepatannya berubah secara teratur. Gerek lurus berubah beraturan tidak terlalu berbeda dengan gerak lurus beraturan. Hanya harga percepatannya saja yang berbeda. Jika pada gerak lurus beraturan percepatannya sama dengan nol, maka pada gerak lurus berubah beraturan tidak sama dengan nol.
Ciri ciri Gerak Lurus Berubah Beraturan :
1. Kecepatannya berubah secara teratur
2. Lintasannya lurus
3. Percepatannya konstan
2. Lintasannya lurus
3. Percepatannya konstan
Untuk memahami gerak lurus berubah beraturan, lakukan kegiatan berikut ini!
Kegiatan :
Gerak lurus berubah beraturan
• Alat dan bahan
1. Mobil mainan
2. Papan luncur
3. Ticker timer
4. Meja
1. Mobil mainan
2. Papan luncur
3. Ticker timer
4. Meja
• Langkah kerja
1. Hubungkan mobil mainan dengan ticker timer (pewaktu ketik), biarkan bergerak
2. Apa yang dapat kamu simpulkan dari rekaman pita ticker timer? Apakah dua titik yang berdekatan pada pita tetap atau berubah– ubah?
3. Hitunglah sepanjang pita ketik dan beri tanda setiap jarak 5 ketikan.
4. Dengan menggunakan gunting , buatlah beberapa potongan setiap jarak 5 ketikan tersebut
5. Susunlah potongan tersebut pada sumbu x – y, seperti gambar di bawah ini.
1. Hubungkan mobil mainan dengan ticker timer (pewaktu ketik), biarkan bergerak
2. Apa yang dapat kamu simpulkan dari rekaman pita ticker timer? Apakah dua titik yang berdekatan pada pita tetap atau berubah– ubah?
3. Hitunglah sepanjang pita ketik dan beri tanda setiap jarak 5 ketikan.
4. Dengan menggunakan gunting , buatlah beberapa potongan setiap jarak 5 ketikan tersebut
5. Susunlah potongan tersebut pada sumbu x – y, seperti gambar di bawah ini.
Ternyata dari percobaan yang dilakukan dapat ditarik kesimpulan bahwa :
- Pada gerak lurus berubah beraturan waktu antara dua titik yang berdekatan pada pita ticker timer selalu berubah-ubah.
- Tinggi tiap potongan 5 ketikan pita ketik pada diagram di atas berbedabeda, ini menunjukkan bahwa benda bergerak dengan kecepatan berubah-ubah.
- Pada gerak lurus berubah beraturan gerak benda dapat mengalami percepatan atau perlambatan. Gerak benda yang mengalami percepatan disebut gerak lurus berubah beraturan dipercepat, sedangkan gerak yang mengalami perlambatan disebut gerak lurus berubah beraturan diperlambat.
- Benda yang bergerak semakin lama semakin cepat dikatakan benda tersebut mengalami percepatan.
Secara matematis percepatan dirumuskan :
a = Δt/t
Keterangan
a = percepatan (m/s2)
Δv = perubahan kecepatan (m/s)
Δv = v2 – v1
v1 = kecepatan awal (m/s)
v2 = kecepatan akhir (m/s)
Keterangan
a = percepatan (m/s2)
Δv = perubahan kecepatan (m/s)
Δv = v2 – v1
v1 = kecepatan awal (m/s)
v2 = kecepatan akhir (m/s)
Kegiatan tersebut di atas menghasilkan grafik kecepatan terhadap waktu pada gerak lurus berubah beraturan sebagai berikut. Nah, jika kemiringan papan luncur diperbesar apa yang akan terjadi? Tentu semakin besar pula garis kemiringan grafik kecepatan terhadap waktu yang dibentuk.
Beberapa peristiwa gerak lurus berubah beraturan dalam kehidupan sehari-hari antara lain, sebagai berikut :
- Gerak mobil yang dipercepat dengan cara menekan pedal gas.
- Gerak mobil yang diperlambat dengan cara menekan pedal rem
- Gerak jatuh bebas buah mangga dari tangkainya
Pada gerak lurus berubah beraturan terdapat 4 rumus utama yang harus dipahami, di antaranya:
1. vt = vo ± at
vt2 = vo2 ± 2as
s = vo.t ± ½ at2
a = Δv / Δt
vt2 = vo2 ± 2as
s = vo.t ± ½ at2
a = Δv / Δt
Dengan:
vt = kecepatan sesaat pada detik ke –t (m/s)
vo = kecepatan awal (m/s)
s = jarak (m)
a = waktu (s)
t = percepatan (m/s2)
tanda ± tergantung pada a, jika a merupakan percepatan maka gunakan tanda tambah (+), dan jika a merupakan perlambatan maka gunakan tanda kurang (-)
vt = kecepatan sesaat pada detik ke –t (m/s)
vo = kecepatan awal (m/s)
s = jarak (m)
a = waktu (s)
t = percepatan (m/s2)
tanda ± tergantung pada a, jika a merupakan percepatan maka gunakan tanda tambah (+), dan jika a merupakan perlambatan maka gunakan tanda kurang (-)
2. Gerak vertikal
Gerak vertikal merupakan salah satu contoh gerak lurus berubah beraturan.
Gerak vertikal merupakan salah satu contoh gerak lurus berubah beraturan.
a. Gerak vertikal ke atas
Karena benda bergerak vertikal ke atas dan berlawanan dengan arah gravitasi bumi maka percepatan bernilai negatif (a = -g ). Ketika benda bergerak ke atas maka kecepatannya akan berkurang seiring dengan perubahan ketinggian pada ketinggian maksimum, kecepatan benda sesaat adalah nol.
Karena benda bergerak vertikal ke atas dan berlawanan dengan arah gravitasi bumi maka percepatan bernilai negatif (a = -g ). Ketika benda bergerak ke atas maka kecepatannya akan berkurang seiring dengan perubahan ketinggian pada ketinggian maksimum, kecepatan benda sesaat adalah nol.
Untuk gerak vertikal ke atas berlaku:
vt = vo – gt
vt2 = vo2 – 2gh
h = vo.t – ½ gt2
Dengan
h = ketinggian
g = percepatan gravitasi
vt = vo – gt
vt2 = vo2 – 2gh
h = vo.t – ½ gt2
Dengan
h = ketinggian
g = percepatan gravitasi
b. Gerak vertikal ke bawah
Merupakan kebalikan dari gerak vertikal ke atas. Benda yang bergerak vertikal ke bawah mengalami percepatan positig (a = g). Kecepatan sesaat pada detik ke- t benda akan lebih besar daripada kecepatan awal.
Merupakan kebalikan dari gerak vertikal ke atas. Benda yang bergerak vertikal ke bawah mengalami percepatan positig (a = g). Kecepatan sesaat pada detik ke- t benda akan lebih besar daripada kecepatan awal.
Untuk gerak vertikal ke bawah berlaku:
vt = vo + gt
vt2 = vo2 + 2gh
h = vo.t + ½ gt2
Dengan
h = ketinggian
g = percepatan gravitasi
vt = vo + gt
vt2 = vo2 + 2gh
h = vo.t + ½ gt2
Dengan
h = ketinggian
g = percepatan gravitasi
3. Gerak jatuh bebas
Gerak jatuh bebas pada dasarnya sama dengan gerak vertikal ke bawah. Namun, pada gerak jatuh bebas, kecepatan awal sama dengan nol sehingga rumus yang digunakan lebih sederhana.
Gerak jatuh bebas pada dasarnya sama dengan gerak vertikal ke bawah. Namun, pada gerak jatuh bebas, kecepatan awal sama dengan nol sehingga rumus yang digunakan lebih sederhana.
Untuk gerak jatuh bebas berlaku:
vt = gt
vt = √(2gh)
h = ½ gt2
Dengan
h = ketinggian
g = percepatan gravitasi
vt = gt
vt = √(2gh)
h = ½ gt2
Dengan
h = ketinggian
g = percepatan gravitasi
Contoh soal
Benda bergerak dengan kecepatan awal 2 m/s, selanjutnya benda dipercepat secara beraturan sehingga kecepatannya menjadi 10 m/s dalam selang waktu 4 sekon. Berapa percepatan yang dialami benda itu?
Benda bergerak dengan kecepatan awal 2 m/s, selanjutnya benda dipercepat secara beraturan sehingga kecepatannya menjadi 10 m/s dalam selang waktu 4 sekon. Berapa percepatan yang dialami benda itu?
Penyelesaian
Diketahui :
v 1 = 2 m/s
v 2 = 10 m/s
t = 4 sekon
Ditanyakan : a = …?
Jawab :
a = Δt/t
Δv = v2 – v1
Δv = 10 m/s – 2 m/s
Δv = 8 m/s
a = 8 m/s / 4 sekon
a = 2 m/s2
Jadi a = 2 m/s2.
v 1 = 2 m/s
v 2 = 10 m/s
t = 4 sekon
Ditanyakan : a = …?
Jawab :
a = Δt/t
Δv = v2 – v1
Δv = 10 m/s – 2 m/s
Δv = 8 m/s
a = 8 m/s / 4 sekon
a = 2 m/s2
Jadi a = 2 m/s2.




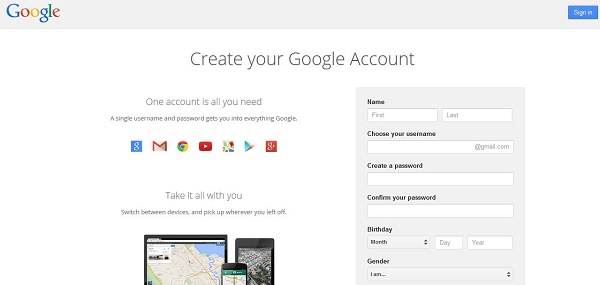
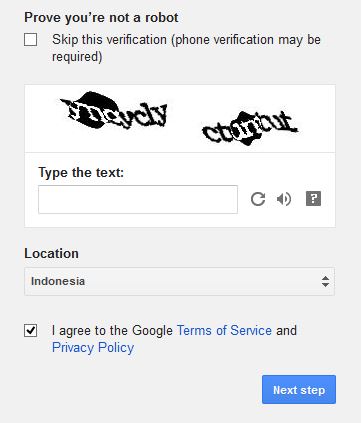
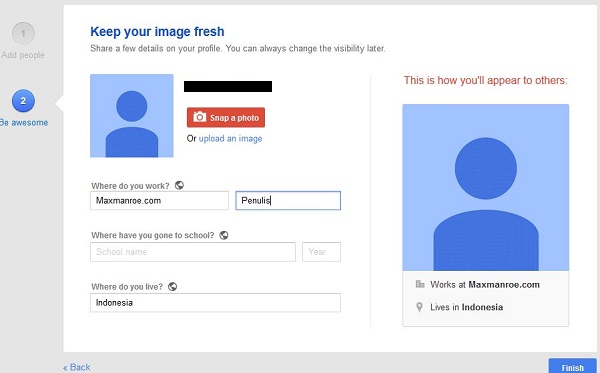
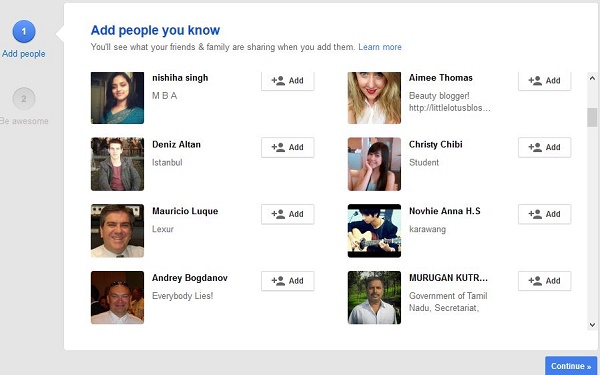 8. Langkah selanjutnya adalah mengisi informasi pekerjaan, sekolah, dan menambah foto profil yang mana informasinya akan ditampilkan di sebelah kanan. Setelah selesai, klik pada Finish dan anda akan diarahkan pada halaman depan google plus.
8. Langkah selanjutnya adalah mengisi informasi pekerjaan, sekolah, dan menambah foto profil yang mana informasinya akan ditampilkan di sebelah kanan. Setelah selesai, klik pada Finish dan anda akan diarahkan pada halaman depan google plus.